Aller au contenu

🔢 De l’ombre des cailloux à la lumière des chiffres

Like 5

Avant même que l’écriture n’existe, l’humanité comptait déjà. Depuis les temps les plus reculés, l’homme cherchait à comparer, à mesurer le monde qui l’entourait, et à conserver la trace de ce qu’il observait.

Le premier « outil » de cette pensée quantitative fut souvent un simple caillou, une pierre déplacée, un nœud dans une corde ou un bâton marqué. Le mot calcul vient d’ailleurs du latin calculus, signifiant « petit caillou ». Le berger déposait une pierre pour chaque mouton sortant du troupeau, établissant une correspondance directe entre deux ensembles : les moutons et les pierres. De ce geste primitif naquit l’idée fondamentale de la numération : un objet ↔ un symbole.

Mais comment sommes-nous passés de ces modestes cailloux à la complexité du système numérique moderne ? L’histoire qui suit raconte la transformation d’un symbole de quantité — le chiffre — en concept abstrait — le nombre. Du simple marquage par encoches à l’invention du zéro, du système additif au système positionnel, chaque étape marque un progrès décisif dans la pensée humaine.

Ce voyage nous conduira du Paléolithique à Bagdad, en passant par l’Égypte, la Mésopotamie, la Grèce, la Chine, l’Inde et la Méso-Amérique. Nous y verrons comment les civilisations ont inventé, adapté et transmis leurs systèmes de comptage, jusqu’à donner naissance aux chiffres que nous utilisons encore aujourd’hui. L’histoire des nombres est, en somme, celle d’un langage universel né du besoin de comprendre le monde.

Les premières traces de la numération préhistorique

Marques, jetons, encoches

Avant toute forme d’écriture, l’humain comptait déjà. Pour garder trace des troupeaux, des stocks de nourriture, des événements ou des cycles lunaires, on trouve des os, des bâtons, des coquillages sur lesquels des marques ont été gravées. Ces objets témoignent de l’émergence d’une pensée numérique : « il y a plus / il y en a moins », « j’ai sorti un animal, j’en ai ajouté un ».

Des os, des bâtons, des coquillages ou des pierres témoignent des premières traces d’un esprit comptable. Par exemple :

  • 🦴 L’os d’Ishango (trouvé au Congo, daté d’environ 20 000 ans avant J.-C.) porte des encoches organisées en groupes, peut-être un début de calendrier ou de comptage.
  • 🐒 Au Swaziland, un péroné de babouin vieux de 30 000 ans porte 29 encoches : peut-être un calendrier lunaire.

Ces traces ne sont pas des nombres « écrits » comme nous les connaissons, mais il s’agit d’un premier pas vers la symbolisation de la quantité.

Os d'Ishango, Institut Royal des Sciences naturelles de Belgique, Bruxelles - Wikimedia Commons, domaine public ou licence CC-BY-SA

Pourquoi ces étapes sont-elles importantes ?

Ces marques de comptage posent les fondations de la numération :

  • la notion de quantité distincte,
  • la mise en correspondance (un objet → une marque),
  • la répétition (multiples objets → multiples marques),
  • et finalement la symbolisation (une marque fixe représente un objet ou un groupe).

Ce stade ne pose pas encore le concept de « nombre » tel que nous l’entendons : il n’y a pas encore de système pour écrire « dix + trois = treize », et on ne parle pas non plus du « troisième » comme d’une idée abstraite, mais seulement du troisième animal, du troisième objet… Cette abstraction apparaîtra plus tard.

“Ecrire un nombre suppose une idée symbolique du monde.”

Transition vers la civilisation organisée

Quand les sociétés se sédentarisent, deviennent agricoles, commercent, bâtissent des cités, le besoin de numération devient plus pressant : calculer les impôts, mesurer les terrains, enregistrer les récoltes, planifier les constructions. Le passage d’un monde de quelques dizaines d’objets à des centaines ou des milliers fait apparaître la nécessité d’un système plus formalisé. Ce sera le terrain de naissance des systèmes classiques de numération.

Compter par paquets :
naissance du système décimal et des autres bases

Il est plausible que le fait que les humains aient dix doigts ait inspiré l’apparition de systèmes à base 10 (décimale). Lorsqu’on compte beaucoup d’objets, on les regroupe par dix pour former un paquet, puis dix paquets pour former un « cent », etc. Ce mode de représentation est intuitif et naturel. Ce système deviendra universel, cependant, d’autres systèmes sont apparus :

  • la base 60 (sexagésimale) : utilisée par les Babyloniens pour les calculs astronomiques et temporels. L’intérêt de cette base est sa richesse en diviseurs (1,2,3,4,5,6,10,12,15,20,30,60) ce qui la rend très pratique pour fractions, divisions, astronomies.
  • la base 20 (vigesimale) : utilisée par les peuples de Méso-Amérique (comme les Mayas), combinant doigts et orteils. L’intérêt de cette base peut être corrélée à la comptabilisation doigts + orteils dans des sociétés où l’usage des pieds était usuel.
  • la base 12 (duodécimale) : mentionnée dans certains contextes historiques, par exemple dans la partition des heures ou des mois. L’intérêt de cette base arrive parfois pour des raisons pratiques (12 mois, 12 heures, 12 pouces…)
  • Base 2 (binaire), utilisée aujourd’hui par les ordinateurs,

Le passage d’un comptage « un-à-un » à un comptage par paquets permet de gérer de plus grandes quantités, de créer des symboles pour des unités, dizaines, centaines, etc. Ce processus mène à la notion de système positionnel (voir section suivante) et à la capacité de faire des calculs complexes.

Les grands types de numération

Avant de plonger dans les systèmes numériques propres à chaque civilisation, il est important de comprendre que chaque peuple développait son propre système de numération, plus ou moins performant selon ses besoins et son niveau de sophistication mathématique.

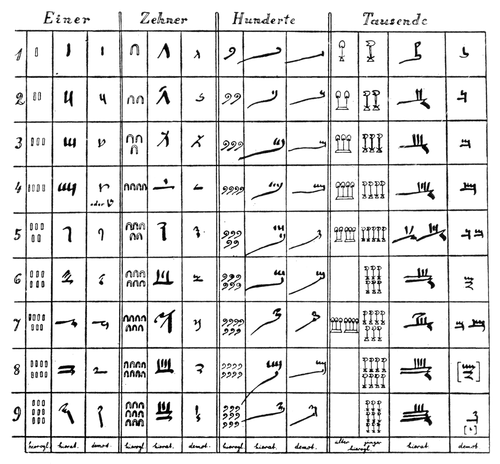
Le principe additif : Dans un système additif, chaque symbole a une valeur précise constante et la valeur d’un nombre est la somme des valeurs des symboles présents. On place essentiellement des symboles côte à côte, on additionne. Exemples : l’Égypte ancienne (un symbole = 100, un autre = 1000, etc.). Le principe additif limite souvent la taille des nombres et rend les opérations longues.

Les limites de ce système apparaissent rapidement, surtout lorsqu’il faut exprimer de grands nombres ou réaliser des opérations. Ce principe était fastidieux pour des calculs élaborait, rendant nécessaire le recours à des outils matériels comme le boulier ou l’abaque pour effectuer les opérations.

Histoire des notations mathématiques, vol. I - Chiffres égyptiens. Symboles numériques hiéroglyphiques, hiératiques et démotiques. (Ce tableau a été compilé par Kurt Sethe.)

Le principe positionnel : Mais alors, une question se pose : comment écrire un nombre en utilisant le moins de symboles possible ? C’est là qu’intervient le principe positionnel, qui constitue l’une des réponses les plus ingénieuses et une avancée majeure dans l’histoire de l’écriture des nombres. 

Dans ce système, la valeur d’un symbole dépend de sa position dans le nombre, ce qui facilite grandement la manipulation des grandes quantités.

Par exemple, dans notre système décimal moderne, le nombre 232 se lit comme suit : 2×100 + 3×10 + 2×1. L’apparition de ce principe a véritablement révolutionné les calculs, permettant une écriture compacte, des opérations rapides, ainsi qu’un système intégré pour la multiplication et la division.

Le principe hybride : Certaines civilisations ont adopté un principe mixte, appelé numération hybride. On dit qu’ils sont hybrides car ils combinent : l’aspect positionnel (la valeur d’un symbole dépend de sa position – comme notre système décimal) et l’aspect additif (à l’intérieur d’une position, les valeurs sont additionnées à l’aide de symboles répétés – pas un seul symbole unique pour chaque valeur comme dans le système décimal moderne). Autrement dit, la valeur totale d’un nombre dépend à la fois de la position des symboles et de l’addition des symboles dans chaque position. 

Nombres babyloniens

Par exemple, le système babylonien. Dans cette notation, chaque symbole ou groupe de symboles représente une valeur multipliée selon sa position, et la somme de ces valeurs donne le nombre final. Ce mécanisme montre comment les systèmes hybrides permettent de coder des nombres complexes tout en conservant la logique positionnelle. Pour illustrer ce fonctionnement, le nombre 753 pourrait s’écrire dans un tel système sous la forme : 710051031. Le système de numération hybride, comme celui des Babyloniens, est plus complexe que les systèmes purement positionnels modernes. Toutefois, certains aspects, notamment la division sexagésimale pour mesurer les angles, sont encore utilisés dans l’astronomie et la géographie en raison de leur intérêt pour le calcul circulaire et angulaire.

Principe Définition Exemple historique Caractéristiques principales
Additif Chaque symbole a une valeur fixe ; on additionne les symboles pour obtenir le nombre. Égypte ancienne : 𓏺 (1), 𓎆 (10), 𓍢 (100), 𓆼 (1000) Simple à concevoir, mais écriture longue et calculs complexes.
Positionnel La valeur d’un symbole dépend de sa position dans le nombre. Inde, puis monde arabo-musulman : 232 = 2×100 + 3×10 + 2×1 Écriture compacte, calculs rapides, base du système décimal.
Hybride Combine les principes additif et positionnel. Babylone : base 60, symboles cunéiformes selon la position. Transition entre les deux systèmes, structure complexe.
Zéro Symbole marquant l’absence de valeur et support du principe positionnel. Inde (vers le Ve siècle), diffusé par les Arabes. Permet la numération complète, l’algèbre et les calculs modernes.

Ainsi, chaque civilisation a mis en œuvre ces principes à sa façon.

🔍 Pour aller plus loin : Les chiffres à travers les civilisations

Découvrez comment ces principes se sont incarnés dans les grandes cultures du monde :

🏺 Mésopotamie – Aux origines des nombres en Mésopotamie – (à paraître en 14 février 2026)

🐫 Égypte ancienne – Compter en hiéroglyphes dans l’Égypte antique – (à paraître en 14 avril 2026)

🐉 Chine – L’art des chiffres dans la Chine ancienne – (à paraître en 14 mai 2026)

🌞 Mayas – Voyage au cœur des nombres Mayas – (à paraître en 14 octobre 2026)

🕉️ Inde – L’Inde : Berceau de la numération moderne – (à paraître en 14 décembre 2026)

🏛️ Grèce et Rome – Quand les lettres servaient à compter dans l’Empire Gréco-Romain – (à paraître en 14 janvier 2026)

📊 Synthèse – Exploration comparative des numérations anciennes – (à paraître en 14 février 2027)

Chaque article explore en détail la manière dont chaque civilisation a façonné sa propre vision du nombre.

🧭 Une série d’articles à lire dans l’ordre ou selon vos envies, pour comprendre comment le monde entier a inventé le langage universel des nombres.

L’héritage universel des nombres

Le passage du concret à l’abstrait

Au fil du temps, la numération est passée de la marque sur pierre à la notation symbolique, puis à la manipulation abstraite. Aujourd’hui, un nombre comme « π » ou « e » n’a plus rien à voir avec des objets concrets : il s’agit d’un concept. Mais derrière cette abstraction se trouvent des millénaires d’invention technique et culturelle.

 

Le rôle du zéro, du positionnel et des bases

Notons de manières non exhaustive, trois innovations majeures :

  • Le zéro (comme marqueur du vide ou absence de valeur) : souvent considéré comme l’un des plus grands sauts de la pensée.

  • Le système positionnel : rendre la valeur dépendante de la place dans l’écriture.

  • Le choix de base : base 10, 60, 20… chacun avec ses avantages et contextes.

Ces innovations ont permis le développement de l’algèbre, du calcul, de l’astronomie, de l’informatique. Leurs racines sont dans les civilisations que nous avons parcourues.

 

Pourquoi cela importe aujourd’hui ?

  • Notre système numérique actuel est un héritage direct de l’Inde et du monde arabe.

  • Les divisions du temps, de l’angle sont héritées de la Mésopotamie.

  • La compréhension que « un nombre peut être représenté » est universelle : cela a déclenché des mathématiques modernes, la physique, l’économie, l’informatique.

  • Lorsque nous manipulons des nombres négatifs, des fractions, des nombres irrationnels, nous marchons sur les épaules de milliers d’années d’invention.

Réflexion culturelle

Chaque système numérique porte en lui la culture de la civilisation qui l’a inventé : sa vision du monde, sa langue, sa religion, ses besoins pratiques. Comprendre l’histoire des nombres, c’est aussi comprendre l’histoire de l’humanité.

Pour résumer : du symbole à la pensée abstraite

L’histoire des chiffres est l’un des récits les plus fascinants de la pensée humaine : elle débute par des marques simples sur des os, se poursuit par des symboles gravés dans la pierre ou l’argile, puis par des bâtonnets manipulés sur une table, et aboutit à nos chiffres modernes que tout enfant apprend en primaire.

Cette histoire n’est pas une simple curiosité : elle montre comment l’humanité a appris à abstraire, à modéliser, à calculer. Le passage des « chiffres » (symboles de quantité) aux « nombres » (concepts manipulables) marque un tournant essentiel. Et cette histoire ne s’arrête pas ici. Elle s’étend vers : les nombres décimaux, les fractions, les nombres irrationnels, les nombres négatifs, l’infini, …

Pour en savoir plus :