Théorème de l’angle au centre

HISTOIRE

L’histoire du théorème de l’angle au centre remonte à l’Antiquité. Euclide, dans son célèbre ouvrage “Les Éléments”, écrit vers 300 avant notre ère, énonce et démontre plusieurs propriétés des cercles et des angles. Les bases de cette propriété sont présentes dans les propositions et les postulats de l’ouvrage (Livre III.20). Au fil des siècles, ce théorème a été étudié, discuté et utilisé par de nombreux mathématiciens et géomètres pour résoudre des problèmes de géométrie et pour approfondir la compréhension des cercles et des angles dans divers contextes mathématiques.

PROPRIÉTÉ

Propriété : “Dans un cercle, un angle au centre mesure le double d’un angle inscrit interceptant le même arc.”

Exemple : Sur la figure ci-contre, l’angle bleu et rouge interceptent le même arc de cercle. Ainsi, l’angle bleu est de double de l’angle rouge.

Télécharger la figure dynamique au format GeoGebra.

DEMONSTRATION

La propriété peut se démontrer de la manière suivante au collège :

Pour démontrer ce théorème, considérons les trois cas suivant, selon la position du centre du cercle par rapport aux côtés de l’angle inscrit :

1^er cas : le centre est situé sur un des côtés de l’angle inscrit.
2^e cas : le centre est situé entre les deux côtés de l’angle inscrit.
3^e cas : le centre n’est pas situé entre les deux côtés de l’angle inscrit.

Dans chaque cas, notons D un point du cercle diamétralement opposé au point M.

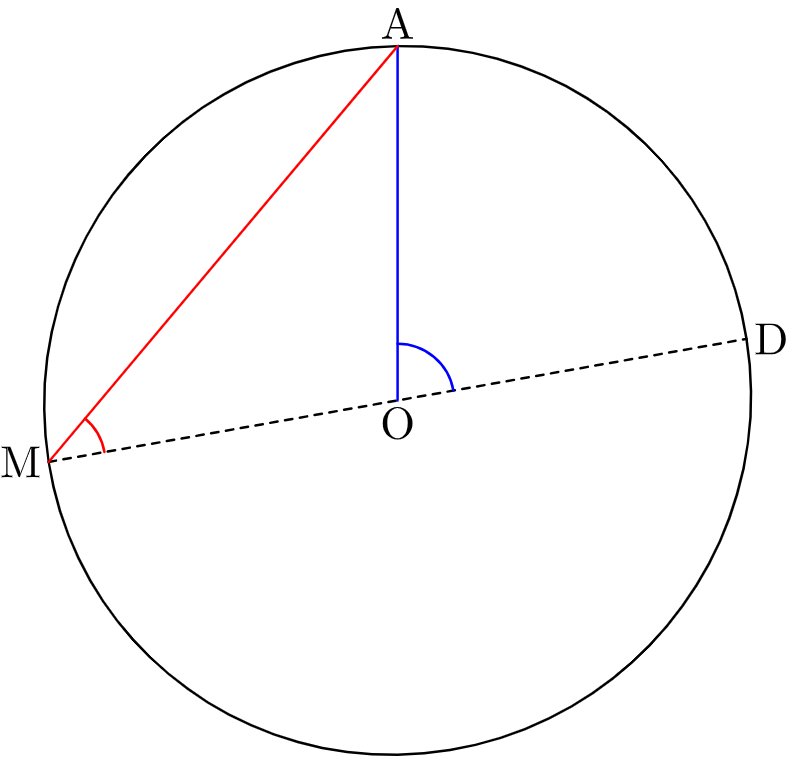
Cas n°1 :

\(\widehat{MOA}\) + \(\widehat{AOD}\) = 180°
De plus, comme O appartient au segment [MD]), alors \(\widehat{AMO}\) = \(\widehat{AMD}\)
Comme le triangle MOA est isocèle en O, alors \(\widehat{MOA}\) + 2\(\widehat{AMO}\) = 180°
Ainsi : \(\widehat{AOD}\) = 180° – \(\widehat{MOA}\)
D’où \(\widehat{AOD}\) = 2\(\widehat{AMO}\)
Donc \(\widehat{AOD}\)= 2\(\widehat{AMD}\)

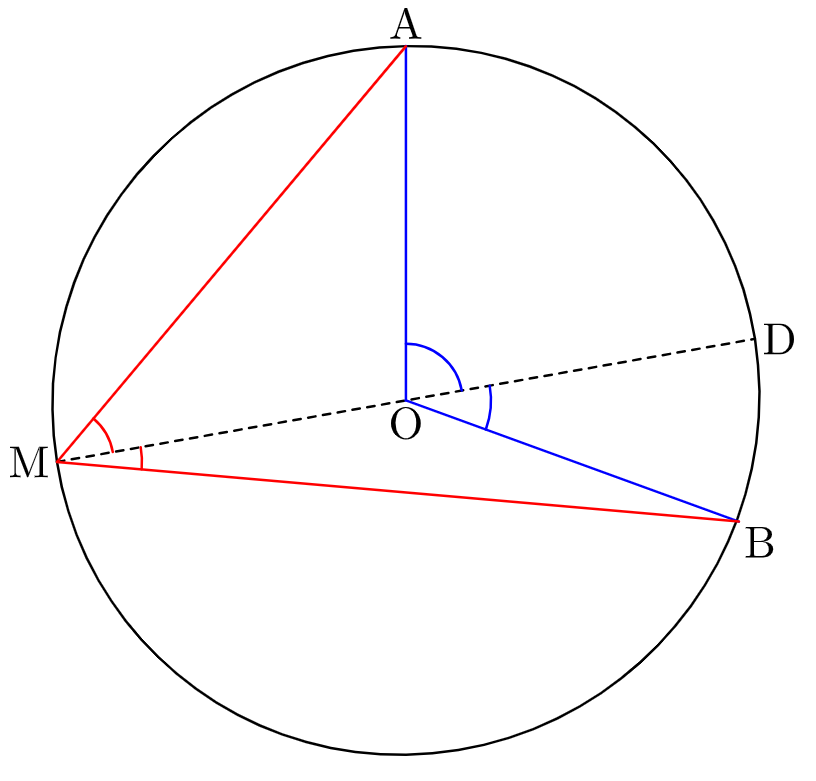
Cas n°2 :

D’après le cas n°1, \(\widehat{AOD}\) = 2\(\widehat{AMD}\).
De même, \(\widehat{DOB}\) = 2\(\widehat{DMB}\).
Donc par somme : \(\widehat{AOB}\) = 2\(\widehat{AMD}\).

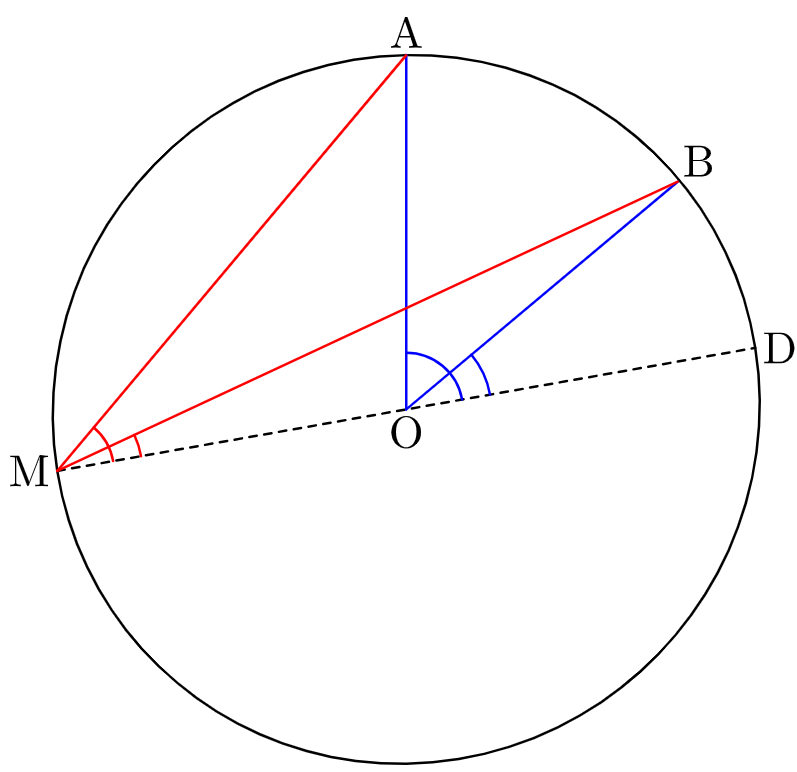
Cas n°3 :

Même raisonnement que dans le cas n°2, en remplaçant “somme” par “différence”.

INTÉRÊT

Aujourd’hui, le théorème de l’angle au centre continue d’être un concept clé enseigné dans les cours de géométrie et est largement utilisé dans les domaines des mathématiques pures et appliquées. Par exemple, ce théorème est à la base de la notion de cercle de focalisation, ou cercle de Rowland, en spectrométrie. Son importance dans la résolution de problèmes géométriques en fait l’un des théorèmes les plus fondamentaux et les plus utiles de la géométrie euclidienne.