L’imagerie médicale, notamment l’Imagerie par Résonance Magnétique (IRM) et la tomographie, repose sur des principes mathématiques fondamentaux pour produire des images détaillées du corps humain et faciliter le diagnostic et le traitement des maladies. Regardons quelques brefs exemples des l’applications des mathématiques dans ces technologies de pointe.
L’IRM (Imagerie par Résonance Magnétique)
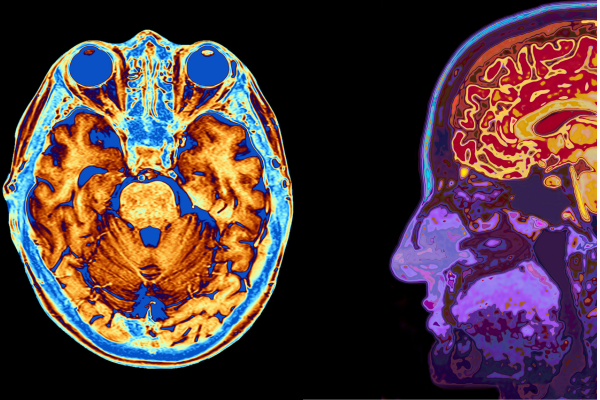
L’IRM est une technique d’imagerie non invasive qui utilise des champs magnétiques et des ondes radio pour générer des images tridimensionnelles des organes et des tissus mous du corps humain. Les mathématiques jouent un rôle crucial à plusieurs niveaux dans le processus d’acquisition et de reconstruction des images par IRM :
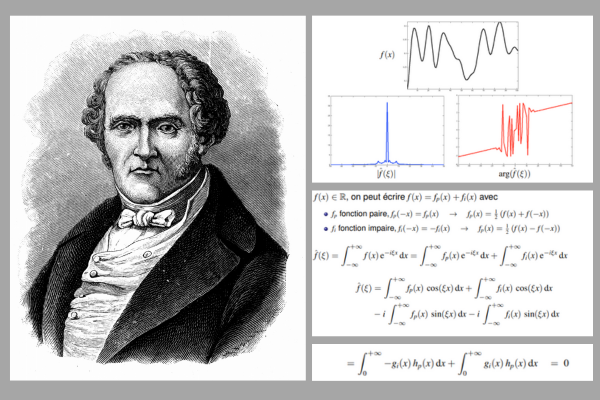
- Transformée de Fourier: L’IRM repose sur la transformée de Fourier, une technique mathématique qui décompose les signaux complexes en leurs composantes de fréquence. En IRM, les signaux provenant des tissus corporels sont transformés de l’espace temporel en espace fréquentiel, ce qui permet de produire des images détaillées.
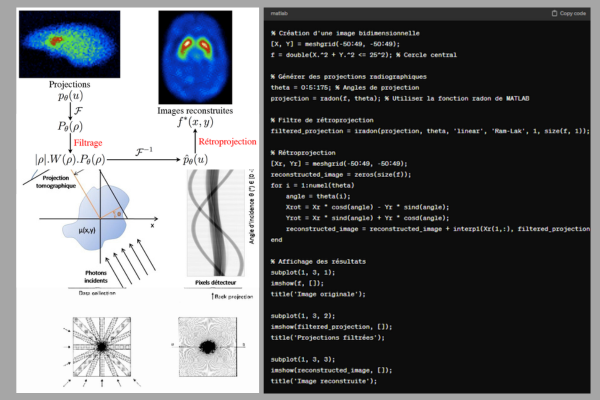
- Rétroprojection filtrée: Pour reconstruire une image en IRM, les données recueillies par le scanner doivent être transformées de l’espace de Fourier en espace spatial. La rétroprojection filtrée est une méthode mathématique utilisée pour effectuer cette transformation, en prenant en compte la géométrie de l’IRM et en appliquant des filtres appropriés pour améliorer la qualité de l’image.
- Algorithme de reconstruction d’image: Une fois les données brutes acquises, des algorithmes de reconstruction d’image sophistiqués sont utilisés pour convertir ces données en images tridimensionnelles précises. Ces algorithmes exploitent des techniques mathématiques avancées telles que la régularisation, la minimisation de l’erreur quadratique et la déconvolution pour améliorer la résolution spatiale et réduire les artefacts d’image.

La Tomographie
La tomographie est une technique d’imagerie médicale qui reconstruit des images tridimensionnelles à partir de coupes transversales ou axiales du corps. Les mathématiques jouent également un rôle central dans la tomographie, en particulier dans la tomographie par rayons X et la tomographie par émission de positrons (TEP) :
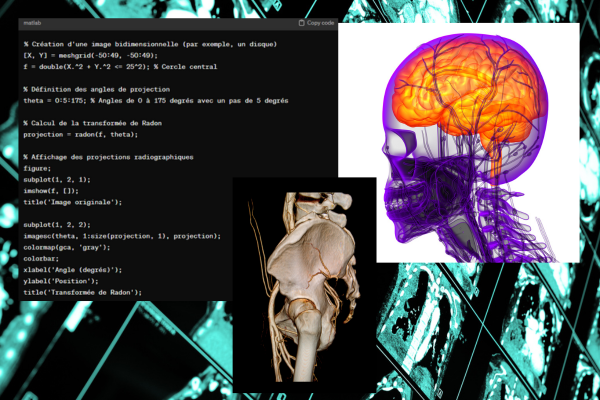
- Transformée Radon: La transformée de Radon est une opération mathématique fondamentale utilisée dans la tomographie par rayons X pour reconstruire une image tridimensionnelle à partir de projections bidimensionnelles. Cette transformée permet de déterminer la densité des tissus corporels en mesurant l’atténuation des rayons X à travers le corps.
- Algorithme de rétroprojection filtrée: Tout comme en IRM, la rétroprojection filtrée est également utilisée en tomographie pour reconstruire des images à partir de données projetées. Cet algorithme mathématique est essentiel pour compenser les effets de l’absorption des rayons X et produire des images anatomiquement précises.

- Analyse statistique et reconstruction itérative: Dans la tomographie par émission de positrons (TEP), les données sont acquises à partir de la détection de photons émis par des radionucléides. L’analyse statistique et la reconstruction itérative sont des techniques mathématiques utilisées pour reconstruire des images TEP en tenant compte du bruit statistique et en optimisant la résolution spatiale.
En conclusion, l’application des mathématiques dans l’IRM et la tomographie est essentielle pour acquérir, traiter et reconstruire des images médicales de haute qualité. Ces technologies démontrent le mariage réussi entre les avancées mathématiques et médicales, offrant aux professionnels de la santé des outils précieux pour le diagnostic, le suivi et le traitement des patients.