Archimède, fils de l’astronome Phidéas, était un mathématicien, physicien, ingénieur, inventeur et astronome grec ancien, né à Syracuse en Sicile vers 287 avant J.-C. et décédé vers 212 avant J.-C. Célèbre pour ses contributions exceptionnelles aux mathématiques et à la physique, ainsi que pour ses inventions et ses découvertes dans divers domaines, il est souvent considéré comme l’un des plus savants de l’Antiquité. Ses découvertes nous ont été transmises par des lettres qu’il a envoyé aux mathématiciens célèbres de son époque.
En mathématiques, Archimède est connu pour différentes découvertes, en voici quelques-unes des plus célèbres :
- La méthode de l’exhaustion1 : Archimède a développé une méthode innovante pour calculer des aires et des volumes en utilisant ce qu’il appelait la méthode de l’exhaustion. Cette méthode consistait à diviser une figure géométrique complexe en un grand nombre de petites régions plus simples, puis à estimer l’aire ou le volume total en additionnant les aires ou volumes de ces régions élémentaires2.

- La quadrature de la spirale : Archimède a étudié la spirale d’Archimède, une courbe générée par le mouvement d’un point le long d’une ligne droite en rotation autour d’un point fixe. Il a déterminé une méthode pour calculer la longueur de cette spirale.
- Le calcul des surfaces et des volumes : Archimède a développé des méthodes pour calculer les aires de surfaces courbes et les volumes de solides géométriques, notamment le cylindre, le cône et la sphère.

- Le calcul de π (pi) : Il est aussi connu pour avoir donné une approximation très précise (3,14185) du nombre Pi. Il s’inspire d’ailleurs de la méthode d’exhaustion en inscrivant et en circonscrivant des polygones réguliers autour d’un cercle. En augmentant le nombre de côtés des polygones, il a pu obtenir des approximations de π de plus en plus précises.
Télécharger la figure dynamique au format GeoGebra.
En physique, Archimède est surtout connu pour son principe de la poussée d’Archimède, qui explique pourquoi les objets flottent ou coulent dans un liquide, ainsi que pour ses études sur les leviers et les forces appliquées.
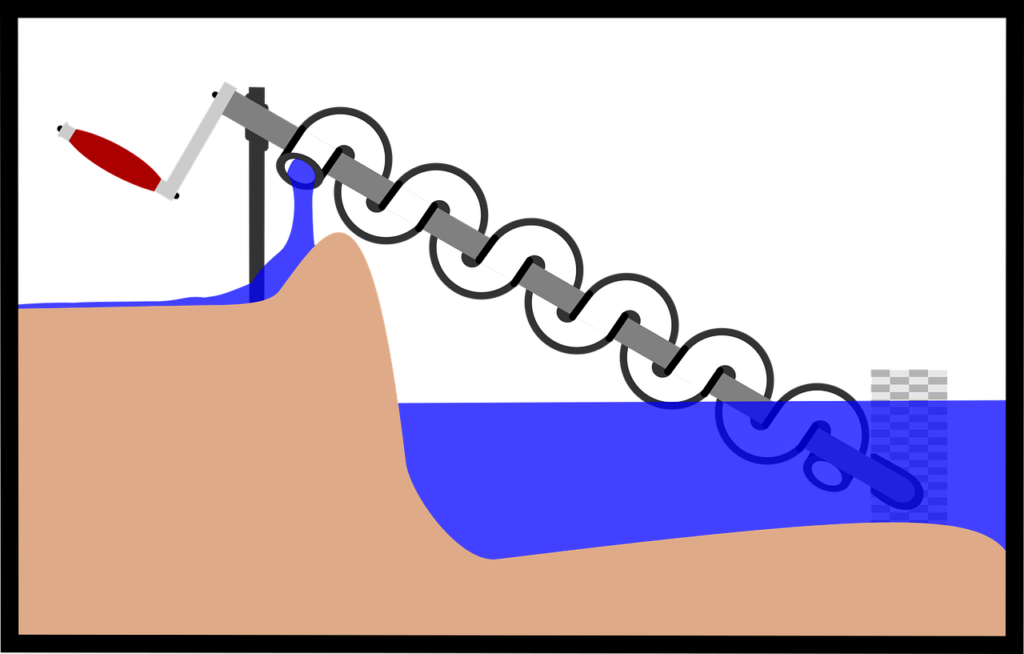
Parmi ses inventions, on trouve le célèbre vis d’Archimède, un dispositif utilisé pour lever l’eau, ainsi que diverses machines de guerre conçues pour défendre Syracuse contre les attaques romaines.
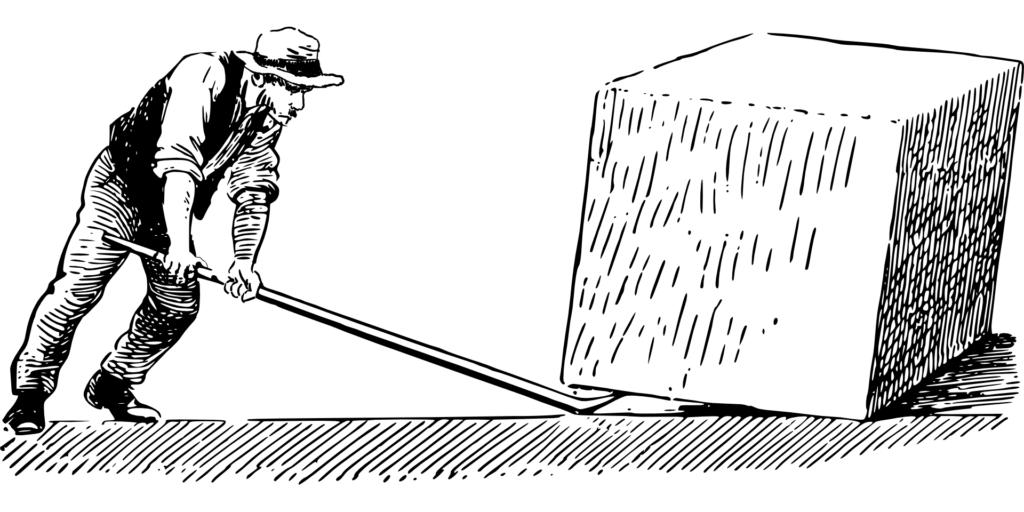
Célèbre citation attribuée à Archimède :
“Donnez-moi un point fixe et un levier et je soulèverai la Terre.”
Archimède est également réputé pour ses travaux en astronomie, notamment ses estimations de la taille et de la distance des objets célestes, ainsi que pour ses contributions à la géométrie et à la mécanique.
La mort d’Archimède est entourée de légendes et de diverses versions, mais la version la plus largement acceptée est qu’il aurait été tué lors de la prise de Syracuse par les Romains en 212 avant J.-C. Pendant ce siège, Archimède était profondément absorbé dans ses travaux mathématiques et aurait ignoré les ordres d’un soldat romain qui lui aurait ordonné de se rendre. Selon la tradition, un soldat romain l’aurait alors tué, bien que le général romain Marcellus aurait été contrarié par cette perte, affirmant qu’il aurait souhaité l’épargner. Cependant, il est important de noter que ces récits sont basés sur des sources historiques anciennes et peuvent contenir des éléments de fiction ou de mythologie.
En résumé, sa vie a été marquée par des découvertes exceptionnelles et des réalisations remarquables qui ont eu une influence profonde sur le développement ultérieur des sciences et des mathématiques. Archimède reste l’une des figures les plus éminentes et les plus respectées de l’histoire des mathématiques et de la science.
Pour en savoir plus :
1Cette Méthode de l’exhaustion serait due à Eudoxe de Cnide (-408 ; -355).
2Ensuite, il faisait varier la taille de ces régions élémentaires jusqu’à ce qu’elles deviennent infinitésimales, de sorte que la somme de leurs aires ou volumes approchait la valeur recherchée. Cela revient à approximer la figure géométrique complexe par des figures plus simples et mieux connues, et ainsi à obtenir une estimation de l’aire ou du volume souhaité. Cette méthode a été un précurseur important du calcul infinitésimal développé plus tard par les mathématiciens tels que Newton et Leibniz.

